Viginere Breaker

A couple of months ago, I wrote a program that breaks Viginere ciphers as a hobby project. It opens a text file containing some ciphertext I generated using a Wikipedia page and cryptii and attempts to decode it by using letter frequency analysis. It’s pretty dumb (doesn’t check if the decoded text actually contains real words) but that’s what the user is for, right? To use it, just download the code from Github and run BreakViginere.py. It will automatically read in the Ciphertext.txt file and start analyzing the cipher. The key I encoded the plaintext with is very complicated, so the first several key guesses will be incorrect. The reason why is that the program is looking for patterns that repeat within the ciphertext. If you don’t know how a Viginere cipher works, it’s pretty simple.

The easiest way to think about how a Viginere cipher works is to use a grid:

If we wanted to encipher the message “Hello World”, we first have to choose a key. A key can be any sequence of letters. Let’s say our key is “BAT”. To encode the message, we write the key over the message and repeat it as many times as is necessary to end up with a one to one correspondence between message letters and key letters. Then, for each pairing of letters, we look up the corresponding ciphertext letter in the grid.

B	A	T	B	A	T	B	A	T	B
H	E	L	L	O	W	O	R	L	D
I	E	E	M	O	P	P	R	E	E

After enciphering the plaintext with our key, the resulting message is “IEEMO, PPREE!”. To decode the message, we follow the same process, except using the ciphertext and the key. So, how can we decode a message without the key? The best way to understand the process is to see how it can be done with a simpler cipher, the Caesar cipher.

The Caesar cipher is likely the simplest method for enciphering a message. All you need to do to encode a message using a Caesar cipher is to shift every letter by the same amount. For example, using a shift of 3 letters, the word “zebra” becomes “cheud”. To decode the message, just shift every letter back by the same amount. Where the interesting part comes in is when you don’t know how many letters to shift the message back by but want to decode the message anyway. One way is to just try every shift. A shift of 26 is the same as not shifting the message at all, and every shift amount higher than that has the same effect as shifting by that amount mod 26, so the number of possible shifts the message could have been encoded is limited to 25. This works for small messages, but for large ones, the difficulty of decoding the message 25 times becomes too high. This is especially a problem for computers because without downloading some kind of dictionary for the program to look words up in, there is no way for the program to know if the message has been successfully decoded without asking a person.

So, instead of checking every possible shift, we can instead take advantage of the fact that not every letter appears in normal English with the same frequency. These are the frequencies of letters in English according to Cornell University:

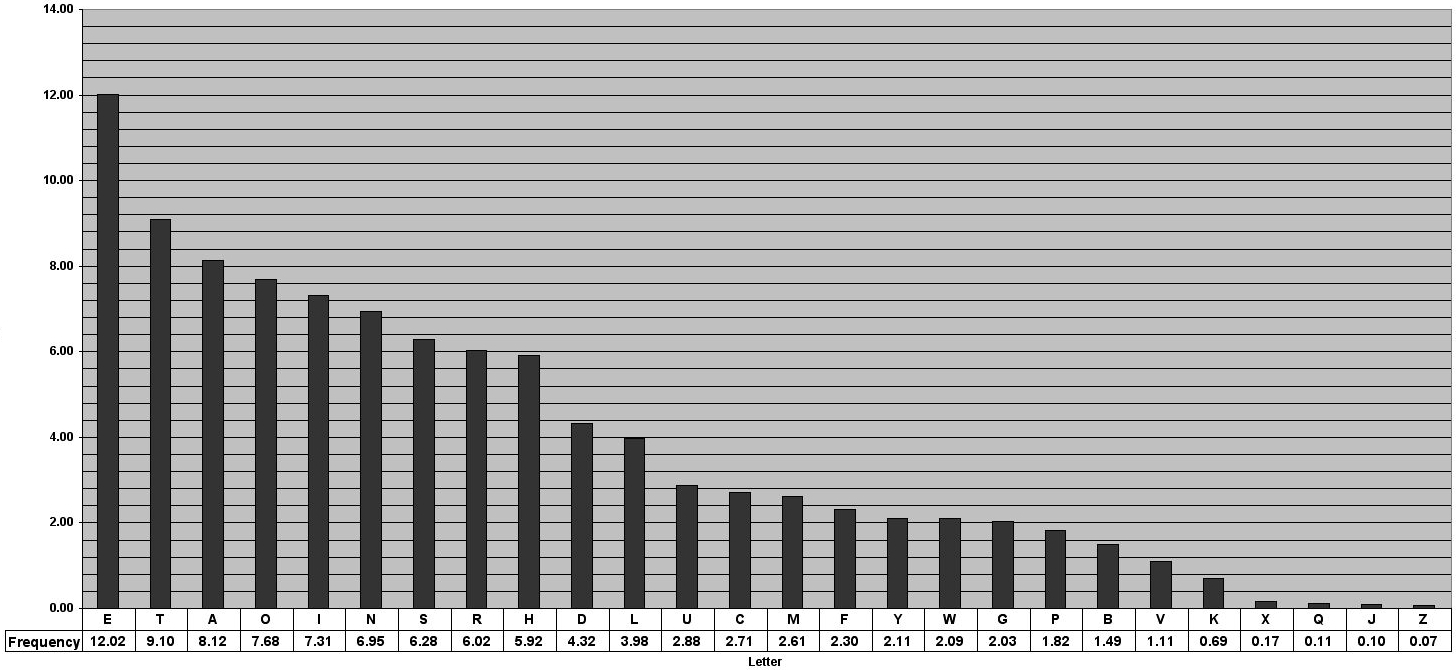
As you can see, the letter E appears far more often than other letters, with a gradual dropoff in frequency until it reaches J and Z, which account for ~0.1% of the letters in every word. Here’s where the useful part is: when we shift every letter in a message by the same amount, the frequencies with which letters appear in the message doesn’t change. All that changes is which letters occur with those frequencies.

Take this message for example: “I will be going to the grocery store with my friends in three hours. Is there anything you need?” This is the letter frequency chart for this sentence.

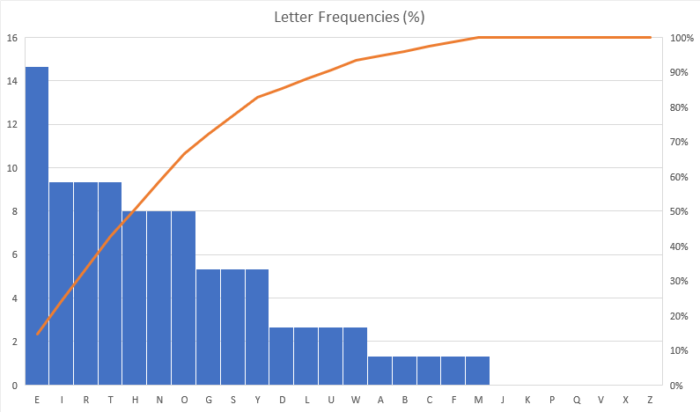
The chart isn’t as smooth as Cornell’s, and the letters aren’t in exactly the same order because there aren’t very many letters in the example sentence, but it still matches the letter frequencies we would expect pretty well. If we shifted every letter in that sentence by 3 places so that the message becomes: “L zloo eh jrlqj wr wkh jurfhub vwruh zlwk pb iulhqgv lq wkuhh krxuv. Lv wkhuh dqbwklqj brx qhhg?” The frequency chart changes to this:

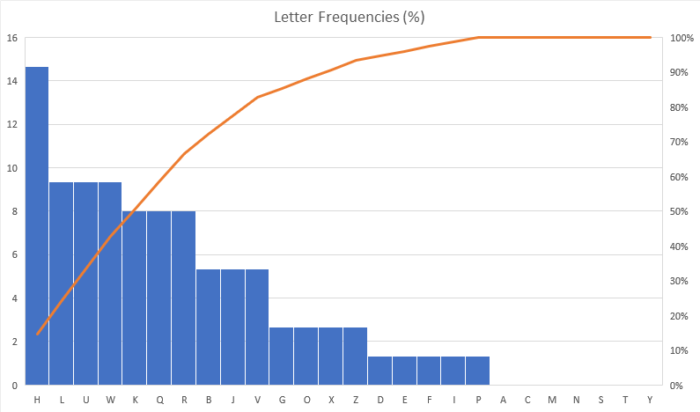
As you can see, the letter frequencies have remained exactly the same. All that has changed is which letters those frequencies are associated with now. To decrypt the message, we find which shift minimizes the root-mean-square error between the frequencies of letters in the message and the frequencies we expect. (For those that don’t know, the RMSE is the square root of the average of the sum of the squared errors. See the Wikipedia article for a more in-depth explanation.) I ran this sentence through the analysis program I wrote, and this is the RMSE between the calculated letter frequencies and the expected letter frequencies for each shift amount:

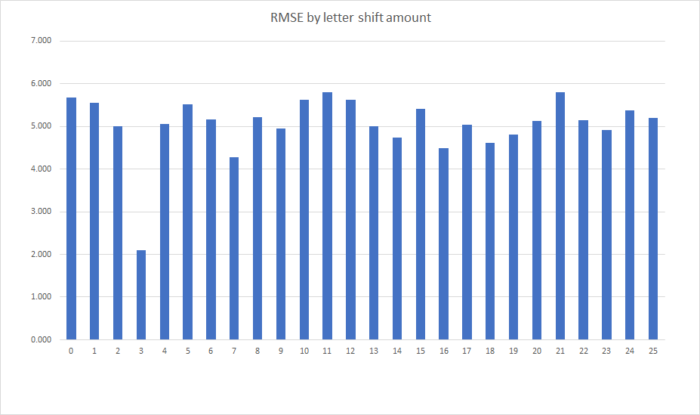
As you can see, the error drops significantly for a shift of three letters, which is how many letters I actually shifted the message by. But how does this help us crack the Viginere cipher? After all, not every letter is shifted by the same amount when we encode a message using it, so there wouldn’t be a clear drop in error like there is with a simple Caesar cipher. The trick is to realize that as long as the message is longer than the key, many parts of the message will be encoded using the same key letter. If we can break the message down into the parts that were encoded with each key letter, we can use the same technique to crack each part as we use to crack a Caesar cipher. To demonstrate, let’s reuse the message I encrypted using the Viginere cipher earlier.

B	A	T	B	A	T	B	A	T	B
H	E	L	L	O	W	O	R	L	D
I	E	E	M	O	P	P	R	E	E

In this example, the H, L, O, and D in the message have all been enciphered using the same key letter: B. The same is true for E, O, and R using A, and L, W, and L using T. If we knew the key was three letters long, we could split this message up into the group of letters that were enciphered with the first key letter, the group that was enciphered with the second letter, and the group enciphered with the third letter and crack each one separately as a Caesar cipher. We already know how to crack a Caesar cipher, so the last step is to figure out how to determine the length of the key without knowing the key or what the message says. But how is that even possible? Consider this sentence encoded using the key “bat”:

The boy and the girl played with the ball and a rope.
Bat bat bat bat batb atbatb atba tba tbat bat b atba
Uhx cor bnw uhx hikm pebyxe wbuh mie uble bnw b rhqe

Common words like “the” and “and” appear several times in this sentence, and with one exception, they are encoded using “bat” every time. As a result, the sequences “uhx” and “bnw” appear several times in the ciphertext too. If we track the number of characters that occur between these patterns, it will tend to be a product of the key length. Of course, this is highly dependent on the random chance of words lining up with the key repetitions, so it doesn’t work very well with short messages. However, as the message gets longer, it becomes increasingly easy for computers to analyze the patterns that appear in the ciphertext and guess the key length.

Once we know the key length, we can split the message up into the parts that were encrypted using one letter of the key, and perform a frequency analysis to determine what letter it is. If we do that for every letter of the key, we can then we can put the letters back together and decrypt the message. It’s a long process, but a computer can run the calculations necessary to accomplish this in less than a minute. In fact, the piece of my program that takes the most time is actually the part that prints the information out for the user! The actual computations are done in a matter of seconds.

If you want to try running it yourself, install python and download the code on Github.